少し前の記事で、老後資金計画のシミュレーションを行いました。ちょっと不必要にマニアックでしたが。
ただ、問題はこれだけでは終わりません。平均的な家計の場合、ベースラインでは資金不足、しかし年金の繰り下げやNISA投資で少し安心という結果でしたが、問題はここからどうするか。資金が足りないからと言って、必要以上に支出を抑えすぎるのは「生活の質」の観点でも避けたい。資金の余裕がある場合も、無駄に資金を残すのは非効率。
死ぬときにちょうど資産がゼロになる「最適支出計画」を探ろうというのが、この次の問題です。まぁ、机上の空論ではありますが、ちょっと考えてみましょう。
「Die with zero」という考え方
以前から話題になっている「Die with zero」という本があります。多くの高齢者が、引退後もお金を使わず、結局、亡くなる際に多額の資金を使い残しているのが実情。だから死ぬまでに自分の楽しみのためにちゃんとお金を使い、ちょうどゼロになるのが最も幸せな生き方だ、というような本です。
まぁ、そりゃそうなんですが、定年後に「自分へのご褒美」とか言って豪華海外旅行、自動車買い替え、自宅リフォーム等にお金を使ってしまい、気が付いたら老後破綻危機に陥りました、みたいなストーリーはネットにあふれています。
ではどれぐらいの支出が「ちょうどいい」のかを考えようと思っても、今後のインフレがどうなるかも、資産運用のリターンも、またいつ自分が死ぬかも分からず、単純な計算はできない。
私はこの本を手に取った際、この辺りの技術的な解決法でも論じているのかと思ったのですが、全く書いてないことに愕然。この本を書いた人も、そのお友達も、まぁ、我々からすればとんでもない金持ちばかり。そりゃ、そんだけの金があれば、色々と金を使った後、最晩年になっても調整の糊代があるわな、と白けてしまいました。
資産の取り崩し法については、定額法ではなく定率法がいい、というアドバイスも聞きます。確かにその方が、途中で資金が尽きました、という事態は避けやすいでしょう。
でも例えば30年でほぼゼロにまで取り崩そうとすれば、年間の取り崩し率は18%となります。現在の資産残高が、いわゆる「富裕層=1億円」の人の場合、初年度の取り崩し額は1800万円になってしまいます。いくら富裕層とはいえ、1年でこれだけのお金を使うのは大変です。
逆に現在の資産残高1000万円であれば、初年度の引き落としは年間180万円でいい感じ。しかし10年目に引き落とせるのは、わずか30万円(1000万円×(1-18%)^9×18%≒30万円)。年間30万円(=月2.5万円)じゃ生活の足しにならん、と言われそう。
やはり富裕層であれ、厳しい層であれ、消費支出がある程度、平準化するような形にしたいはず。うまく30年後に資産をゼロにするためには、どれぐらいの支出にすればいいのか、ある程度のガイダンスが必要なのではと思うわけです。
前回のシミュレーションを逆に使えないか?
そこで、前回のシミュレーションを逆に使って考えてみます。
前回の枠組みは、現時点の支出額(これは既知数)を出発点として、90歳や100歳時点の資産残高(これが未知数)を計算するものでした(インフレ率などは一定の範囲内でランダムに動くとして)。これを逆に使って、100歳時点の資産残高を一定の目標額(例えば0円:これが既知数)にするような現時点の支出額(こっちが未知数)を計算すればいいわけです。
実質消費額の経路は逆ロジスティック型で定まるので、現時点の消費額を仮置きすれば、今後100歳まで年々の「実質消費額」は定まります。ここにインフレ率等のシナリオを与えれば、名目支出額も計算され、最終時点の資産残高も計算できます。これを使えば、現時点の最適消費額が(解析的には無理ですが)反復計算により得られます。
インフレ率等のランダム変数があるため、計算結果は現時点での最適消費額の分布として得られます。インフレ率等の想定が1万通りあれば、Die with zero目標に対応した現時点の消費額も1万通り計算されます。この「最適解」分布の中央値辺りなら、ほぼDie with zeroになりますよ、という指針にはなるのではないでしょうか。
ということで、それをやってみました。前回のシミュレーションだと、1万回のシナリオでも2~3秒で計算は終わりますが、こっちはもう少し時間がかかり、40秒ほどを要します。まぁ許容範囲かなと思います。
最適値の選択の考え方
ここでは100歳時点で100万円を残すことを目標にします。0円でもいいのですが、最後の最後、何があるか分かりませんし、自分の葬式代ぐらいは残しておこうと考える人は多いでしょう。
計算された最適解(計算結果の分布の中央値)を使って検算すると(つまり前回と同じシミュレーションをすると)、100歳時点の資産残高の分布は、この目標値(100万円)を中央値とした分布になっていることが確認できます。
人生の最後で絶対に貧窮したくないと思う人は、この分布の大半がゼロより右側にいることを望むかもしれません。その場合、最適消費額も、中央値ではなく例えば25パーセンタイル値(現時点の消費額は小さくなる)を選べば、より安全になります。
この場合、高い確率で資産を使い残すことになるため「Die with zero」の方針とは齟齬が出ますが、それも本人の選択とは言えます。
試算結果
まずベースケースとして、65歳から年金受給し、NISA投資をしない場合で計算します。この時の現在の最適消費額は23.7万円となりました。現在の消費支出が25.7万円なので、毎月2万円ほど節約する必要があります。
次に年金受給を1年遅らせる場合は、現在の最適消費額は24.8万円に増えます。ベースケースより1万円ほど改善しますが、まだ現状支出額より1万円弱の削減が必要。
最後にNISAのみの場合は24.2万円。ベースケースよりは5000円の余裕がありますが、やはり現状に比べての節約が必要になります。
この計算結果を前回のシミュレーションに用いて検算してみます。以下は繰り下げ受給の場合の資産分布と資産の推移です。100歳時点の資産残高の中央値は約100万円と、目標達成できそう。もしゼロ円を目標にして計算すれば、中央値がゼロ円、破綻確率は50%となっているはずです。
破綻確率は20%ありますが、最終時点での貯蓄残高を減らそうと思えば、これは避けられません。
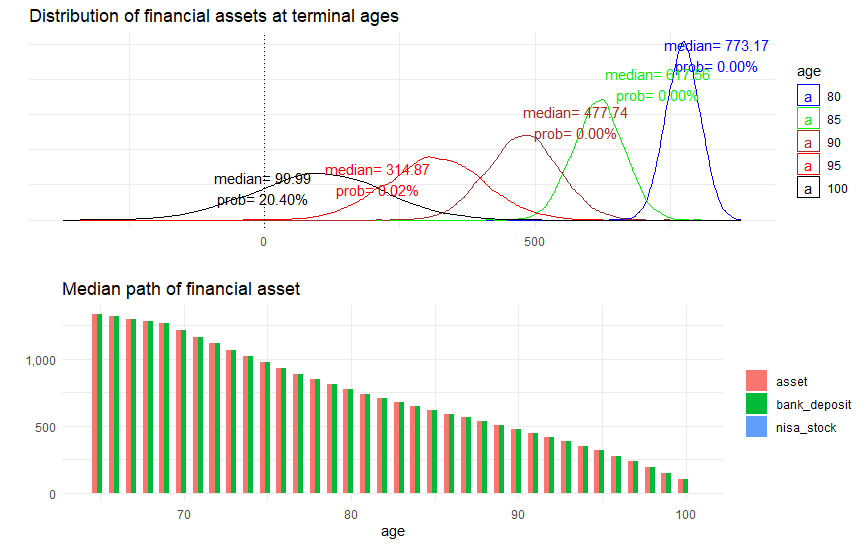
では、ここでもう少し余裕を出すため、年金を69歳まで繰り下げてみます。
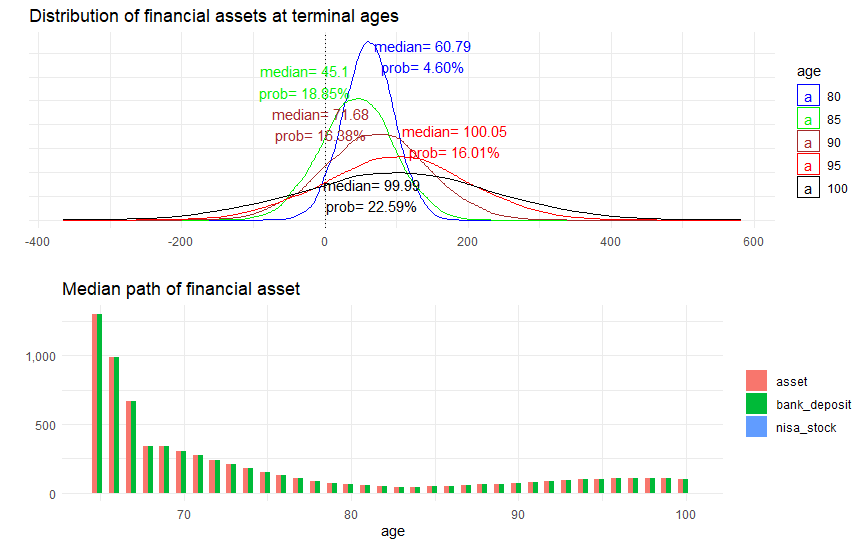
この場合、現在の最適消費額は27.7万円と、2万円ほど余裕が出てきます。しかし、その一方で年金繰り下げ期間中の預金取り崩しが大きいため急激に預金は減少し、84歳時点での資産残高はわずか44万円。その後、低い水準で、ただし微妙に増える状態で推移し、100歳時点での資産残高が目標通り100万円となります。
老後、何が起きるか分からない、という点でのリスクを考えると、このような資産経路が「安心」と言えるかどうかは、かなり人によって違うかなと思います。
定率法との比較
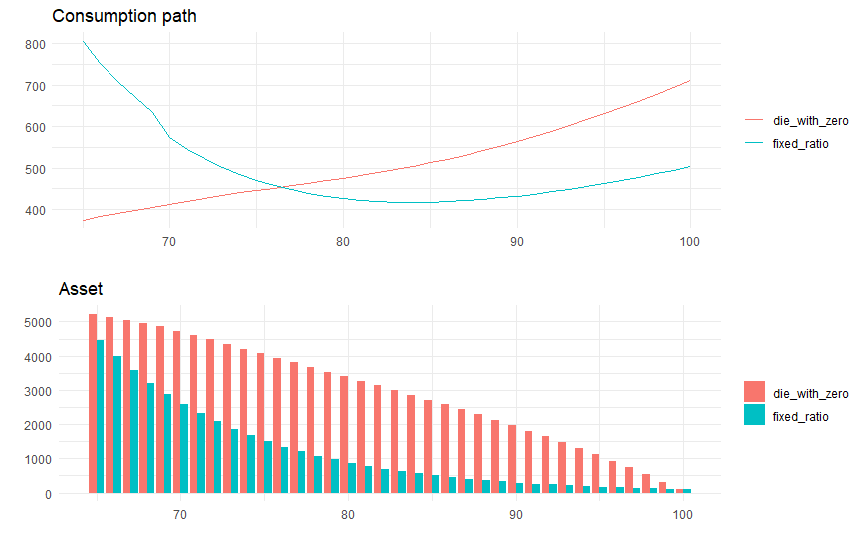
最後に今回の試算方法と資産定率取り崩し法の比較をしてみます。ここでは現時点での資産が5000万円という準富裕層を考えます。
Die with zeroの場合、今期の最適消費額は月額30.5万円となります。
一方、定率取り崩しの場合、100歳時の資産を100万円にしようとすれば、毎年の資産の取り崩し率は10.9%となります。つまり、この取り崩し額に年金+勤労所得を加えたものが総支出額、ここから税金等の非消費支出を引いたものが消費支出額となります。
この2つのケースでの消費額と資産残高の推移を比較したのが以下の図。定率法の場合、消費額(年間)は初年度の805万円から75歳時に470万円、81歳時には最小の423万円となった後、100歳時には503万円へと徐々に伸びていきます(インフレ込みの名目値なので、実質消費は大きく減額しています)。
一方、上記のDie with zeroシミュレーションの場合は、インフレのためコンスタントに上昇していますが、動きは平準化しています(実質では逆ロジスティック型の緩やかな減額)。やはり私ならシミュレーションのほうが安定していいですね。
とはいえ、これはあくまでシミュレーション。前提のインフレの範囲を超えて、インフレが進んだり、マクロスライド制度が途中で変わったりと、何事も「これですべて想定済」とはいかないのが現実。
まぁ、実際には早い時点では中央値を採用するより、25パーセンタイルや30パーセンタイルの消費水準を選び、その後、年齢が進むにしたがって中央値に移っていくというように、年齢を通じての調整が正しいようには思います。
しかし、まぁ、こんな作業をすることで、何となく「Die with zero」の達成に向けた目安ができると言えるかもしれません。お粗末様でした。