以前、日本の相続税の状況を見ました。その際、本当はお金持ちの遺産が、どれぐらい世代間の資産格差につながっているか、逆に相続税でどの程度、格差が是正されているかを見たかったのですが、いいデータが見つかりませんでした。
仕方ないので、今回はよく使われる「Yard sale model」というシミュレーション枠組みを利用して、相続税によりどれぐらい格差が是正されるか試してみようと思います。
必ずしも現実世界がこういうものだと言いたいわけではなく、「ちょっと面白い遊びをしてみよう」程度のものですが、お付き合いください。
基本のYard sale model
まず作業のベースとなる「Yard sale model」というモデルについて、簡単に説明します。例えば100人のプレイヤーがいる世界を考え、当初、全員が100円ずつ資産を持っているとします。ここでランダムに2人を選び出して、コイン投げを行います。手元資産の一部(例えば20%)を掛け金として拠出して、勝った方が負けた方の掛け金を全部取得します。
最初のころは、選び出された2人とも資産は同額の100円なので掛け金も同額ですが、しばらくすると以前のコイン投げの結果により2人の手許資産が変わってきます。その場合、資産の少ない方を掛け金の基準にし、金持ちのほうも同額の掛け金を拠出します。例えば2人の手元資産が50円と150円だったら、50円×20%=10円をそれぞれの掛け金とします。金持ちの掛け金は、150円×20%=30円ではありません。
このゲームでは、当初の資産は全員同額の100円、コイン投げの確率も同率なので、ゲームを続けていっても、資産分布はグニョグニョと動きつつ、ほぼ平等な水準で推移すると思いそうなのですが、実は資産保有額は大きく偏っていきます。
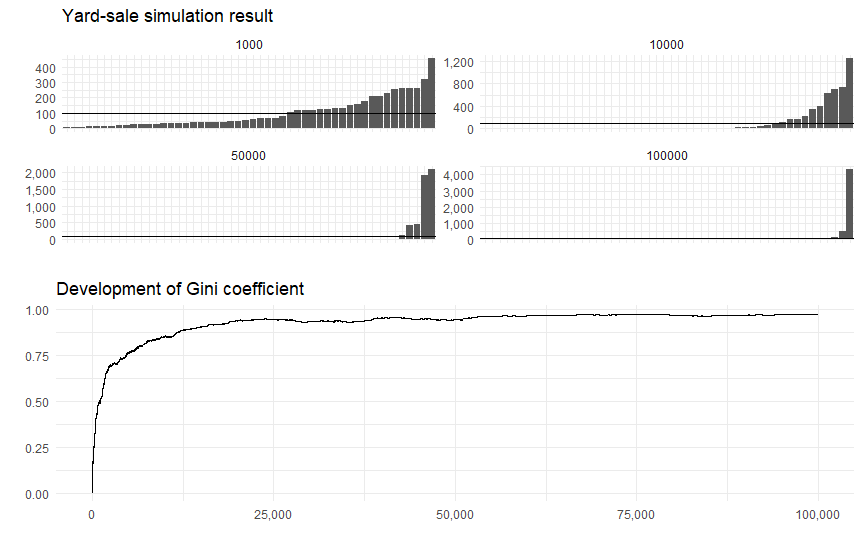
グラフの上パネルは、このゲームを10万回繰り返した場合の資産分布ですが、1000回目、1万回目、5万回目と、ゲームを繰り返すにつれて資産分布はどんどん偏っていき、10万回目にはほぼ1人に資産が集中することになります。
下のパネルは、このゲームで資産保有額のジニ係数の推移を計算したものです。当初のゼロ(完全平等)から急激に配分は悪化し、最終的には1(完全不平等)に近い水準で、ずっと推移します。
もちろん、誰が「超大金持ち」になるかは完全にランダムであり、同じゲームを最初からやり直した場合、2回目、3回目に大金持ちになる人間は異なります。
このように、完全に同じ条件でのゲーム(経済取引)なのに、全くの偶然(コイントスの勝敗)から、ここまでの資産の集中、不平等化が進むというのが、このモデルの面白いところですが、逆に現実世界ではここまでの資産集中はないので、現実味という点では課題が残ります。
少しモデルを変えてみる
このモデルは、最終的に資産が極端に集中する状態までもっていきたいため、毎回2人ずつ抽出して1対1の勝負をし、掛け金は資産の少ない方に合わせる、という設計にしているところがミソです。ただ、このために試行回数をかなり繰り返さないといけません。つまり計算に時間がかかってしまいます(私のコード・スキルの限界のせいですが)。
そこで勝手な解釈ですが、計算時間を節約し、またもう少し現実的な資産分布にするため、少し枠組みを修正してみます。
今回は毎回、全員参加のコイン投げを行います。掛け金は自分の持っている資産の一定比率とします。資産額が異なれば、掛け金の比率は同じ、つまり掛け金額は資産額に比例します。掛け金率を20%とするなら、100円を持っている人は20円、1000円を持っている人は200円です。コイン投げの結果、各人の勝ち負けが決まると、敗者からの掛け金没収分を、勝者が掛け金に応じて按分して(つまり元の資産保有額に応じて)受け取ります。
これを繰り返すと、それほど回数を経ないでも、かなりの資産保有の格差が生まれますが、基本モデルほどの独占状態にはなりません。そういう意味では、少し現実に近いと言えるかもしれません。
ここで相続税をモデルに追加します。このゲームを200回行いますが、毎回、ランダムに選ばれた2割のプレイヤーに税金が課され、資産の再分配を行います。平均以上の資産を持つ人は、平均からの超過分の一定割合を徴収され、平均以下の資産を持つ人に平均からの不足分に応じて配分される、という制度です。資産が多い人ほど、絶対額では多額を徴収され、資産が少ない人ほど絶対額で多くを受け取れる、ただし再分配前の資産から逆転することはない、ということですね。
平均5回に1回の資産再分配なので、1回のゲームが10年程度の経済取引を表し、5回(50年ほど)終わったところでプレイヤーが亡くなり、子供に資産が引き継がれる、その際に一定程度の相続税がかかるという感じをイメージしています。
シミュレーション結果
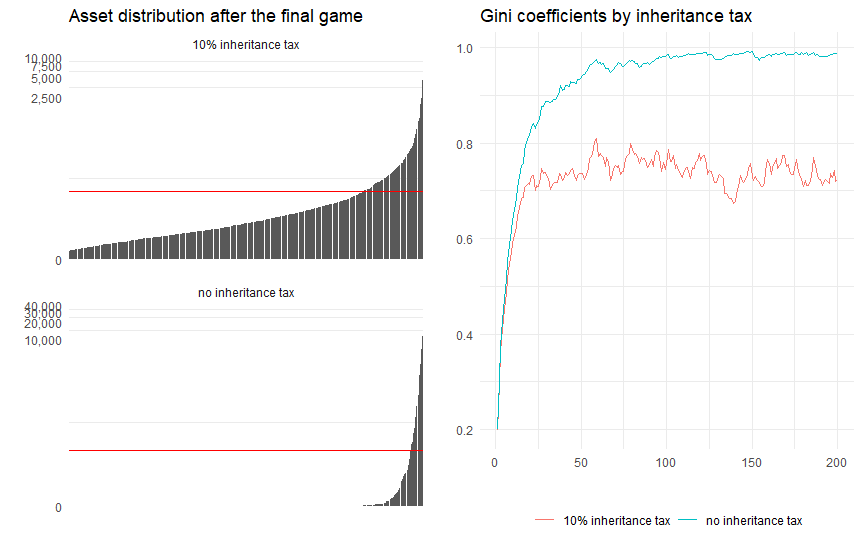
まず相続税がない場合とある場合とで、どう資産分布が変わるかを見てみます。以下は掛け率を保有資産の40%として、相続税がないケースと10%が課されるケースを比較したものです。
左パネルが200回施行後の資産分布ですが(赤線が当初資産額の100円)、相続税がある場合は最も豊かな人で7,600円ちょっと、最も貧しい人で5円です。一方、相続税がないと最低はほぼ0円(10のマイナス12乗ぐらい)、最高は30,000円強です。
右パネルがジニ係数の推移ですが、相続税がない場合は最終的に0.98、10%の相続税を課すと0.72前後です。以前使ったWorld Inequality Databaseから全世界の資産格差データを見ると、0.98は最も不平等な南ア(0.95)より上に相当します。一方、0.72ぐらいだと、デンマークやスペインといった国(かなり低い方)に相当します。日本の資産分布のジニ係数は0.74ぐらいです。
平均以上の資産を持つ人に、その平均との差の10%だけの相続税を課すというのは、そんなに重税という感じもしませんが(個人の感想です)、それで南アからデンマークぐらいまでに資産格差を是正できるのであれば、相続税というのは十分に効果的な感じはします。
資産分布の不平等を解消する上では、掛け金の比率を変えることでも可能です。経済取引のギャンブル性を落とすということですね。こっちについては是非の判断は分かれるかもしれません。少々リスクが高くても、リターンの可能性も高い経済のほうがいいだろう、という考えはありえます。
一応、このゲームは敗者の掛け金が没収され、その分、勝者が掛け金に応じて受け取るという設計なので、基本はゼロサム・ゲームです。このため、掛け金率は完全にギャンブルの程度を表す指標になります。この辺り、本当は設計を変えたほうが現実に近いのでしょうが、まぁ、そこまで真剣な記事でもないので、ご勘弁を。
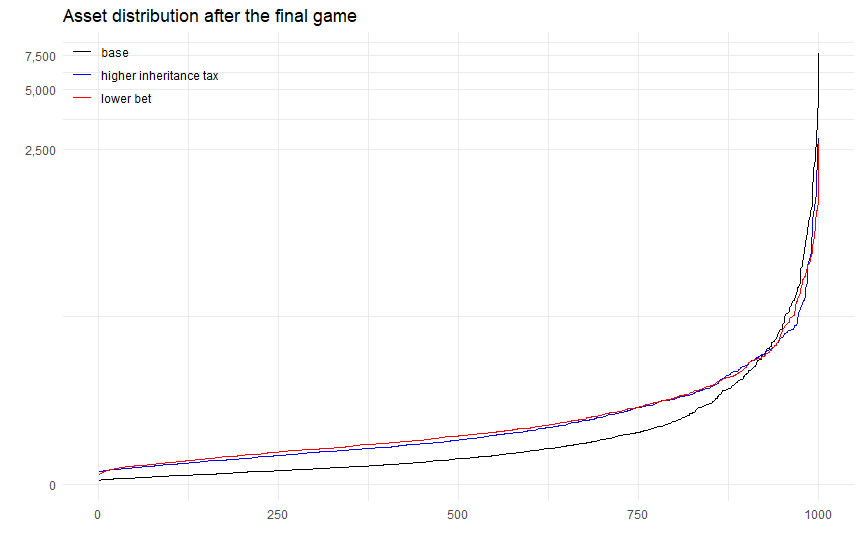
以下はゲームのパラメーターを少し変えた比較です。ベースは掛け金率40%、相続税率10%(上でやった通り)。「higher inheritance tax」は掛け金率40%で、相続税率を30%に上げたもの、「lower bet」は相続税率10%で、掛け金率を20%に下げたものです。
相続税率を上げても、掛け金率を下げても、資産分布の偏りは修正されています。たまたまですが、その修正具合も似ています。
まぁ、格差があること自体、いいか悪いかの議論はあります。頑張った人はちゃんと報われるべきだろうと思います。でも、このゲームもそうですが、ホントは単なる運なのかもしれません。さらに、自身の頑張りや能力ではなく、単に親が金持ちだったから、その子も金持ちを引き継いで、世代間の格差が固定されてしまうのだとすると、また話は変わってきます。この辺りは、また別稿で遊んでみたいと思います。